Quantum Computer.
quantum computer is a device that performs quantum computing. Such a computer is completely different from binary digital electronic computers based on transistorsand capacitors. Whereas common digital computing requires that the data be encoded into binary digits (bits), each of which is always in one of two definite states (0 or 1), quantum computation uses quantum bits or qubits, which can be in superpositions of states. A quantum Turing machine is a theoretical model of such a computer and is also known as the universal quantum computer. The field of quantum computing was initiated by the work of Paul Benioffand Yuri Manin in 1980, Richard Feynman in 1982, and David Deutsch in 1985.
As of 2018, the development of actual quantum computers is still in its infancy, but experiments have been carried out in which quantum computational operations were executed on a very small number of quantum bits. Both practical and theoretical research continues, and many national governments and military agencies are funding quantum computing research in additional effort to develop quantum computers for civilian, business, trade, environmental and national security purposes, such as cryptanalysis.Noisy devices with a small number of qubits, also dubbed noisy intermediate-scale quantum (NISQ) devices by John Preskill,have been developed by a number of companies, including IBM, Intel, and Google.IBM has made 5-qubit and 16-qubit quantum computing devices available to the public for experiments via the cloud on the IBM Q Experience. D-Wave Systems has been developing their own version of a quantum computer that uses annealing.
A recent review by Mikhail Dyakonov in IEEE Spectrum argues that practical quantum computers are not likely to be implemented. He says: "There is a tremendous gap between the rudimentary but very hard experiments that have been carried out with a few qubits and the extremely developed quantum-computing theory, which relies on manipulating thousands to millions of qubits to calculate anything useful. That gap is not likely to be closed anytime soon."
Principles of operation :
A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits. For example, representing the state of an n-qubit system on a classical computer requires the storage of 2n complex coefficients, while to characterize the state of a classical n-bit system it is sufficient to provide the values of the n bits, that is, only n numbers. Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before the measurement. It is generally incorrect to think of a system of qubits as being in one particular state before the measurement. The qubits are in a superposition of states before any measurement is made, which directly affects the possible outcomes of the computation.
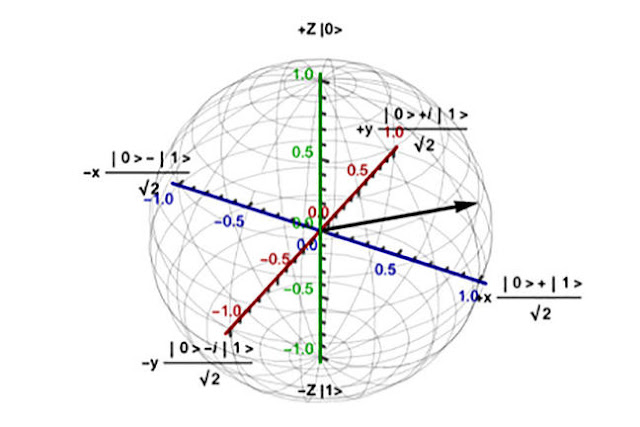
The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.
As of 2018, the development of actual quantum computers is still in its infancy, but experiments have been carried out in which quantum computational operations were executed on a very small number of quantum bits. Both practical and theoretical research continues, and many national governments and military agencies are funding quantum computing research in additional effort to develop quantum computers for civilian, business, trade, environmental and national security purposes, such as cryptanalysis.Noisy devices with a small number of qubits, also dubbed noisy intermediate-scale quantum (NISQ) devices by John Preskill,have been developed by a number of companies, including IBM, Intel, and Google.IBM has made 5-qubit and 16-qubit quantum computing devices available to the public for experiments via the cloud on the IBM Q Experience. D-Wave Systems has been developing their own version of a quantum computer that uses annealing.
Large-scale quantum computers would theoretically be able to solve certain problems much more quickly than any classical computers that use even the best currently known algorithms, like integer factorizationusing Shor's algorithm (which is a quantum algorithm) and the simulation of quantum many-body systems. There exist quantum algorithms, such as Simon's algorithm, that run faster than any possible probabilistic classical algorithm. A classical computer could in principle (with exponential resources) simulate a quantum algorithm, as quantum computation does not violate the Church–Turing thesis. On the other hand, quantum computers may be able to efficiently solve problems which are not practicallyfeasible on classical computers.
Principles of operation :
A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits. For example, representing the state of an n-qubit system on a classical computer requires the storage of 2n complex coefficients, while to characterize the state of a classical n-bit system it is sufficient to provide the values of the n bits, that is, only n numbers. Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before the measurement. It is generally incorrect to think of a system of qubits as being in one particular state before the measurement. The qubits are in a superposition of states before any measurement is made, which directly affects the possible outcomes of the computation.
To better understand this point, consider a classical computer that operates on a three-bit register. If the exact state of the register at a given time is not known, it can be described as a probability distribution over the 2^{3}=8 different three-bit strings 000, 001, 010, 011, 100, 101, 110, and 111. If there is no uncertainty over its state, then it is in exactly one of these states with probability 1. However, if it is a probabilistic computer, then there is a possibility of it being in any one of a number of different states.
The state of a three-qubit quantum computer is similarly described by an eight-dimensional vector (a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7}) (or a one dimensional vector with each vector node holding the amplitude and the state as the bit string of qubits). Here, however, the coefficients ' i ' ( iota) are complex numbers, and it is the sum of the squares of the coefficients' absolute values, {sum _{i}|a_{i}|^{2}}, that must equal 1. For each {i}, the absolute value squared {left|a_{i}\right|^{2}}gives the probability of the system being found in the {i}-th state after a measurement. However, because a complex number encodes not just a magnitude but also a direction in the complex plane, the phase difference between any two coefficients (states) represents a meaningful parameter. This is a fundamental difference between quantum computing and probabilistic classical computing.
Please ! write your suggestions and interested topics in comment box.
If you want more information about this article please cooment in comment box.
Please, subscribe our website to support us to put interesting articles.
If you measure the three qubits, you will observe a three-bit string. The probability of measuring a given string is the squared magnitude of that string's coefficient (i.e., the probability of measuring 000 = {a_{0}|^{2}}, the probability of measuring 001 = {a_{1}|^{2}}, etc.). Thus, measuring a quantum state described by complex coefficients { (a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7})} gives the classical probability distribution { (|a_{0}|^{2},|a_{1}|^{2},|a_{2}|^{2},|a_{3}|^{2},|a_{4}|^{2},|a_{5}|^{2},|a_{6}|^{2},|a_{7}|^{2})}and we say that the quantum state "collapses" to a classical state as a result of making the measurement.
An eight-dimensional vector can be specified in many different ways depending on what basis is chosen for the space. The basis of bit strings (e.g., 000, 001, …, 111) is known as the computational basis. Other possible bases are unit-length, orthogonal vectors and the eigenvectors of the Pauli-x operator. Ket notation is often used to make the choice of basis explicit. For example, the state { (a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7})} in the computational basis can be written as:
{ a_{0}\,|000\rangle +a_{1}\,|001\rangle +a_{2}\,|010\rangle +a_{3}\,|011\rangle +a_{4}\,|100\rangle +a_{5}\,|101\rangle +a_{6}\,|110\rangle +a_{7}\,|111\rangle }where, e.g., { |010\rangle =\left(0,0,1,0,0,0,0,0\right)}
The computational basis for a single qubit (two dimensions) is {\displaystyle |0\rangle =\left(1,0\right)} and {\displaystyle |1\rangle =\left(0,1\right)}.
Using the eigenvectors of the Pauli-x operator, a single qubit is { |+\rangle ={\tfrac {1}{\sqrt {2}}}\left(1,1\right)} and { |-\rangle ={\tfrac {1}{\sqrt {2}}}\left(1,-1\right)}.
Please ! write your suggestions and interested topics in comment box.
If you want more information about this article please cooment in comment box.
Please, subscribe our website to support us to put interesting articles.
Quantum Computer : Future of our Neurological Networking
 Reviewed by A civil Engineer
on
January 20, 2019
Rating:
Reviewed by A civil Engineer
on
January 20, 2019
Rating:
 Reviewed by A civil Engineer
on
January 20, 2019
Rating:
Reviewed by A civil Engineer
on
January 20, 2019
Rating:























No comments: